Given: The simplified value of the equation is 143.
1980 ÷ 9 + [-77 + {-1980 + (1/4 of 7290)}]
Concept used:
BODMAS rule
Calculations:
1980 ÷ 9 + [-77 + {-1980 + (1/4 × 7290)}]
⇒ 1980 ÷ 9 + [-77 + {-1980 + (7290/4)}]
⇒ 1980 ÷ 9+ [-77 + {-1980 + (1980)}]
⇒ 1980 ÷ 9+ [-77 + {-1980 + 1980}]
⇒ 1980 ÷ 9 + [-77 + {0}]
⇒ 220 + [-77]
⇒ 220 – 77 = 143
∴ The simplified value of the equation is 143.
24The population of a country has been growing at a rate of 4% every decade. If the projected population of the country in 2030 is given as 1,58,18,400, what was the population of the country in 2000?
Given:
Population in 2030 = 15818400
Growth Rate = 4% per decade
Concept used:
Amount (A) = Principle (1 + R%)T
Calculations:
According to the question,
A = P(1 + 4%)3
⇒ 15818400 = P(1 + 0.04)3
⇒ P(1.04)3 = 15818400
⇒ P = 15818400/ 1.124864
⇒ P = 14062500
∴ The population of the country in 2000 was 14062500.
23The average speed of a train running at a speed of 30 km/h during the first 100 km, at the speed of 40 km/h during the second 100 km and at the speed of 50 km/h during the last 100 km is nearly _____.
Given:
Speed of train during the first 100 km = 30 km/h
Speed of train during the second 100 km = 40 km/h
Speed of train during the third 100 km = 50 km/h
Concept used:
Time = Distance/Speed
Calcuilations:
According to the question,
Time taken to cover first 100 kilometres = 100/30 = 1/3
Time taken to cover second 100 kilometres = 100/40 = 1/4
Time taken to cover third 100 kilometres = 100/50 = 2
Total Time Taken = 10/3 + 5/2 + 2 = (20 + 15 + 12)/6
Total Time = 47/6
Average speed = 300/(47/6) = 1800/47 = 38.29 ~ 38.30
∴ The average speed of a train is 40 km/h ~ 38.30 km/h
22What is the largest 6-digit number divisible by 52?
Given:
The largest 6-digit number divisible by 52
Calculations:
The largest 6-digit number = 999999
Now the largest 6-digit number divisible by 52
⇒ 999999/52 = 19230.75 with remainder 39
Now,
⇒ 999999 – 39 = 999960
∴ The largest 6-digit number divisible by 52 is 999960.
21The difference between a discount of 35% on ₹8,000 and two successive discounts of 20% and 15% on the same amount is:
Given:
Marked Price = Rs. 8000
First Discount = 35%
Successive discounts on the bill = 20% and 15%
Formula used:
S.P = [(100- Discount% ) /100] × M.P
In case of successive discounts, equivalent discount% = a + b – (ab/100)
Where, a = First discount percentage, b = Second discount percentage
Calculation:
According to the first condition,
⇒ S.P1 = [(100 – 35)/100] × 8000
⇒ S.P1 = 65/100 × 8000
⇒ S.P1 = 0.65 × 8000 = Rs. 5200
According to the second condition,
Equivalent discount = 20 + 15 – (20 × 15/100)
Equivalent discount = (35 – 3)%
Equivalent discount = 32%
⇒ S.P2 = [(100 – 32)/100] × 8000
⇒ S.P2 = [68/100] × 8000
⇒ S.P2 = 0.68 × 8000 = Rs. 5440
Now the difference between the First condition and second condition = Rs. 5440 – Rs. 5200 = Rs. 240
∴ The difference between the First and second discounts is Rs. 240.
2030 men can complete a piece of work in 24 days. 12 days after they started working together, 10 more men joined them. How many days will they now take to complete then remaining work?
Given:
30 men can complete a piece of work in 24 days.
12 days later 10 more men joined them.
Concept used:
Work = Efficiency × Time
Calculations:
According to the question,
Total work = 30 × 24 = 720 units
One day work of 30 men = 1/24 units
12 days work of 30 men = 12 × 1/24 = 1/2 units
12 days later 10 more men joined them,
Total no. of men = 30 + 10 = 40 men
Half of the work is done by 30 men then remaining work = 720/2 = 360 units
Time required to complete 360 units of work by 40 men = 360/40 = 9 days
∴ The remaining work will be completed in 9 days.
199832 – 172 = ?
Given:
9832 – 172 = ?
Formula used:
a2 – b2 = (a + b)(a – b)
Calculations:
(983)2 – (17)2
⇒ (983 + 17)(983 – 17)
⇒ 1000 × 966 = 966000
∴ 9832 – 172 is 966000.
18The following pie chart shows the spending of a country on tourism in various districts during a particular year. Total spending of the country ₹15,62,000
Study the pie chart and answer the following question.
How much less money (in ₹) is spent on district C than on district E ?
Given:
Total spending of the country = ₹15,62,000
Concept used:
Percentage = (Given value/Total value) × 100
Calculations:
According to the question,
Money spent on District C = 14% of total money
⇒ District C = 14% of 1562000
⇒ District C = 14/100 × 1562000
⇒ District C = 14 × 15620 = Rs. 218680
Money spent on District C = 18% of total money
⇒ District E = 18% of 1562000
⇒ District E = 18/100 × 1562000
⇒ District E = 18 × 15620 = Rs. 281160
Now difference between money spent of district C and district E
⇒ (Money spent on District E) – (Money spent on District C)
⇒ (281160) – (218680) = Rs. 62480
∴ Rs. 62480 is spent on District C than on District E.
17In an engineering institution, a student’s grade is assessed based on Internal tests (30%), assignments (30%) and external exams (40%). If a student scored 90% in internal tests, 95% in assignments and 75% in external exams, then the overall
grade of the student is:
Given:
Marks distribution = Internal tests (30%) + Assignments (30%) + External exams (40%) = 100%
Student Scored = 90% of internal test + 95% of Assignments + 75% of external exam
Concept used:
Percentage = (Given value/Total value) × 100
Calculations:
According to the question,
Total percentage (PT) student acquired = 90% of internal test + 95% of Assignments + 75% of external exam
⇒ PT = 90% of 30 + 95% of 30 + 75% of 40
⇒ PT = 90% × 30 + 95% × 30 + 75% × 40
⇒ PT = 0.90 × 30 + 0.95 × 30 + 0.75 × 40
⇒ PT = 27% + 28.5% + 30%
⇒ PT = 85.50%
∴ The overall grade of the student is 85.50%.
16The average present age of four members of a family is 27 years and average increases by 3 years when one of their relatives joins them. The age of the relative is:
Given:
The average present age of four members of a family is 27 years
Average increases by 3 years when one of their relatives joins them
Concept used:
Average value = (Sum of all the values)/Total no. values)
Calculations:
Let the age of relative be 'x'
According to the question,
Average age = [(4 × 27) + x]/5
⇒ 30 = (108 + x)/5
⇒ 108 + x = 150
⇒ x = 150 – 108 = 42 years
∴ The age of the relative is 42 years.
15When f(x) = 15x3 – 14x2 – 4x + 10 is divided by (3x + 2), then the remainder is:
Given:
f(x) = 15x3 – 14x2 – 4x + 10
Calculations:
According to the question,
15x3 – 14x2 – 4x + 10 – Remainder = (3x + 2) Integer
Now
⇒ 15x3 + 10x2 – 24x2 -16x + 12x + 8 + 2
⇒ 5x2(3x + 2) – 8x(3x + 2) + 4(3x + 2) + 2
⇒ (3x + 2)(5x2 – 8x + 4) + 2
⇒ (3x + 2) Integer + 2
∴ The remainder is 2.
14Subir claimed to sell his items at only 5% above the cost of production, but used a weight that had 1 kg written on it, though it actually weighed 960 grams. What was the actual profit percentage earned by Subir?
Given:
Marked Price = 5% above CP
Concept used:
Profit% = (SP – CP)/CP × 100
Calculation:
According to the question,
Let the Cost Price of item be Rs. 1000, then
Marked Up Price = 5% of CP + CP
⇒ MP = 1000 (1 + 5%)
⇒ MP = 1000 × 1.05 = Rs. 1050
But he Sold 960g instead of 1kg for Rs. 1050
Then CP of 960g = Rs. 960
⇒ Profit% = (1050 – 960)/960 × 100
⇒ Profit% = 90/960 × 100 = 9.375%
∴ The actual profit percentage earned by Subir is 9.375%.
13Study the given table and answer the question that follows.
The table shows quanity of various food items used by a restaurant during four months of a year (in kg).
| Food Item | June | July | August | September |
| Rice | 180 | 200 | 240 | 300 |
| Wheat | 420 | 400 | 380 | 350 |
| Sugar | 200 | 210 | 230 | 240 |
| Pulses | 250 | 310 | 320 | 280 |
| Vegetables | 300 | 320 | 390 | 370 |
The quantity of wheat used in the month of July is what percentage of the total quantity of food items used in June ?
Given:
The table shows quanity of various food items used by a restaurant during four months of a year (in kg).
| Food Item | June | July | August | September |
| Rice | 180 | 200 | 240 | 300 |
| Wheat | 420 | 400 | 380 | 350 |
| Sugar | 200 | 210 | 230 | 240 |
| Pulses | 250 | 310 | 320 | 280 |
| Vegetables | 300 | 320 | 390 | 370 |
Calculations:
According to the question,
The quantity of wheat used in the month of July = 400 kg
The total quantity of food items used in June = 180 + 420 + 200 + 250 + 300 = 1350 kg
Now percentage
⇒ (The quantity of wheat used in the month of July)/(the total quantity of food items used in June) × 100
⇒ (400)/(1350) × 100
⇒ 0.2692 × 100 = 26.92% or 29\(\frac{{17}}{{27}}\)%
∴ The quantity of wheat used in the month of July is 26.92% or 29\(\frac{{17}}{{27}}\)% of the total quantity of food items used in June.
12In the given figure, If ∠RPS = 25°, the value of ∠ROS is_______.
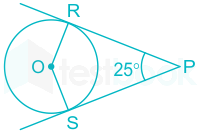
Given:

∠RPS = 25°
∠S = ∠R = 90° [Tangent of a circle is perpendicular to the Radius]
Concept used:
Sum of all the angles of quadrilateral = 360°
Calculations:
According to the question,
in quadrilateral OSPR,
⇒ ∠ P + ∠ S + ∠ O + ∠ R = 360°
⇒ 25° + 90° + ∠ O + 90° = 360°
⇒ ∠ ROS = 360° – 205° = 155°
∴ The value of ∠ROS is 155°.
11The volume of a cone of radius 13 cm is 507 π cm3. Find its height.
Given:
The volume of a cone = 507 π cm3.
Radius (r) of cone = 13 cm
Formula used:
Volume of cone = 1/3 πr2H
Where, r = radius
H = Height
Calculations:
According to the question,
Volume of cone = 1/3π(13)2H
⇒ 507 π = (1/3)×(169 π)H
⇒ H = (507 × 3)/169
⇒ H = 1521/169 = 9 cm
∴ The height of the cone is 9 cm.
10What is the fourth proportional to 16, 24, 8?
Given:
16 : 24 :: 8 : ?
Calculations:
Let the fourth proportion be x
16: 24 :: 8: x
⇒ 16/24 = 8/x
⇒ x = 8 × 24/16
⇒ x = 24/2 = 12
∴ The fourth proportion is 12.
9Which of the following can be a rationalising factor of ( \(\sqrt 2 \) + \(\sqrt 3\) + \(\sqrt 5\)) ?
Given:
(√2 + √3 + √5)
Calculations:
(√2 + √3 + √5)(√2 + √3 – √5) √6
⇒ (2 + √6 – √10 + √6 + 3 – √15 + √10 + √15 – 5)√6
⇒ (2√6)√6 = 12
Here, 12 is rational number
∴ The rationalising factor of (√2 + √3 + √5) is (√2 + √3 – √5)√6.
8The price of a tablet is first increased by 10%, and then decreased by 2.5% due to reduction in sales. What is the net percentage change in the final price of the tablet?
Given:
The price of a tablet is first increased by = 10%
The price of a tablet is then decreased by = 2.5%
Concept used:
Overall discount = (A + B) – (AB/100)
Calculations:
According to the question,
DIscount = (10 – 2.5) – (10 × 2.5)/100
⇒ D = (7.5) – (25/100)
⇒ D = (7.5) – (0.25) = 7.25%
∴ The net percentage change in the final price of the tablet is increased by 7.25%.
7The price of a cell phone is ₹20,000. On Sundays, the shopkeeper offers a cash discount of ₹1,000 on the purchase of the cell phone. Further, if someone purchases it through a credit card, he gives 5% additional discount. If someone is purchasing the cell phone on a Sunday through a credit card, then how much does he/she have to pay?
Given:
Actual price of phone = Rs. 20000
Sunday discount = Rs. 1000
Credit card discount = 5%
Concept used:
Percentage = Lower value/Upper value × 100
Calculations:
According to the question,
Price of Phone on sunday = Actual Price – Sunday discount = 20000 – 1000 = 19000
Price of Phone on sunday with credit card
⇒ Price (1 – Discount%)
⇒ 19000 (1 – 0.05)
⇒ 19000 × 0.95 = Rs. 18050
∴ The price of phone on sunday with credit card on discount will be Rs. 18050.
6A thief is noticed by a policeman from a distance of 650 m. The thief starts running and the policeman chases him. The thief and the policeman run at the rate of 8 km and 10.5 km per hour, respectively. The distance (in metres) between them after 12 minutes is:
Given:
Distance between theif and police = 650 m
Speed of theif = 8 km/h
Speed of police = 10.5 km/h
Concept used:
Speed = Distance/Time
Speed of theif = 8km/h × 5/18 = 20/9 m/s
Speed of police = 10.5km/h × 5/18 = 17.5/6 m/s
Calculations:
According to the question,
⇒ Distance traveled by theif in 12 mins = 20/9 × (12 × 60) = 14400/9 = 1600 m
⇒ Distance traveled by police in 12 mins = 17.5/6 × (12 × 60) = 14400/9 = 2100 m
⇒ Distance between theif and police after 12 mins = (Initial distance + distance traveled by theif in 12 mins) – (Distance traveled by police in 12 mins)
⇒ Distance = (650 + 1600) – 2100 = 2250 – 2100 = 150 m
∴ The distance (in metres) between them after 12 minutes is 150 m.
5The table below gives the numbers (in thousand) of different types of geysers sold by a company in six consecutive years.
| Year | Types | ||||
| A | B | C | D | E | |
| 2007 | 75 | 122 | 103 | 98 | 95 |
| 2008 | 100 | 102 | 103 | 112 | 102 |
| 2009 | 105 | 108 | 112 | 109 | 108 |
| 2010 | 100 | 189 | 123 | 102 | 122 |
| 2011 | 95 | 123 | 102 | 124 | 124 |
| 2012 | 85 | 145 | 134 | 134 | 145 |
What is the difference in the number of type B geysers sold in 2010 and 2012 ?
Given:
The table below gives the numbers (in thousand) of different types of geysers sold by a company in six consecutive years.
| Year | Types | ||||
| A | B | C | D | E | |
| 2007 | 75 | 122 | 103 | 98 | 95 |
| 2008 | 100 | 102 | 103 | 112 | 102 |
| 2009 | 105 | 108 | 112 | 109 | 108 |
| 2010 | 100 | 189 | 123 | 102 | 122 |
| 2011 | 95 | 123 | 102 | 124 | 124 |
| 2012 | 85 | 145 | 134 | 134 | 145 |
Calculations:
According to the question,
The number of type B geysers sold in 2010 = 189000 units
The number of type B geysers sold in 2012 = 145000 units
The difference in the number of type B geysers sold in 2010 and 2012
⇒ 189000 – 145000 = 44000 units
∴ The difference in the number of type B geysers sold in 2010 and 2012 is 44000 units.
4Find the total surface area of a closed hemisphere whose radius is 3.5 cm. (Use π = 22/7)
Given:
Radius (r) of the hemisphere = 3.5 cm
Formula used:
Total surface area of a closed hemisphere = 3πr2
Calculations:
According to the question,
TSA = 3π(3.5)2
⇒ TSA = 3 × 22/7 × 12.25
⇒ TSA = 808.5/7 = 115.5 cm2
∴ The total surface area of a closed hemisphere is 115.5 cm2.
3The frustum of a right circular cone has the radius of the base as 5 cm, radius of the top as 3 cm, and height as 6 cm. What is its volume?
Given:
Radius of the base (R) = 5 cm
Radius of the top (r) = 3 cm
Height (H) of frustum = 6 cm
Formula used:
Volume of Frustum (V) = 1/3 πH (R2 + Rr + r2)
Calculations:
According to the question,

Volume of Frustum = 1/3 π × 6 × [(5)2 + (5 × 3) + (3)2]
⇒ V = π × 2 × [25 + 15 + 9]
⇒ V = π × 2 × [49] = 98π cm3
∴ The volume of frustum is 98π cm3.
2If cos 2A = sin 75°, then the smallest positive value of A is:
Given:
Cos 2A = sin 75°
Concept used:
Cos θ = Sin (90 – θ)
Calculations:
According to the question,
Cos 2A = Sin 75°
⇒ Sin (90°- 2A) = Sin (75°)
Removing Sin From LHS and RHS
⇒ 90° – 2A = 75°
⇒ 2A = 90° – 75°
⇒ 2A = 15°
⇒ A = 15/2 = 7.5°
∴ The smallest positive value of A is 7.5°.
1In an election, there were three candidates: A, B and C. 10% of the eligible voters did not vote. Out of those who voted, 45% voted for A, 35% voted for B and the remaining 20% voted for C. 30% of the votes polled for A and 20% of the votes polled for B were later deemed invalid, while all the votes polled for C were deemed valid. If A got 882 more valid votes than B did, how many valid votes did C receive?
Given:
45% voted for A, 35% voted for B and the remaining 20% voted for C.
30% of the votes polled for A and 20% of the votes polled for B were later deemed invalid,
A got 882 more valid votes than B
Calculations:
According to the question,
Let the total votes be 'x'
882 = (Valid votes of A) – (Valid votes of B)
⇒ 882 = (70% of 45% of 90% of x) – (80% of 35% of 90% of x)
⇒ 882 = (x × 90 × 10 × 5)/1000000 (7 × 9 – 8 × 7)
⇒ 882 = (4500x)/1000000 × (63 – 56)
⇒ 882 = (45x)/10000 × (7)
⇒ x = (882 × 10000)/(7 × 45)
⇒ x = 14 × 2000 = 28000 votes
Now, valid votes did C recieve
Votes of C = 20% of 90% of valid votes
⇒ Votes of C = 20% × 90% × 28000
⇒ Votes of C = 0.20 × 0.90 × 28000
⇒ Votes of C = 0.20 × 25200 = 5040 votes
∴ Valid votes of C is 5040.
0